ELECTRICAL UNIT CONVERSION

NEW!!! NEW!!! NEW!!! POWER CONVERSION CALCULATORS
BE SURE TO CHECK OUT OUR NEW POWER CONVERSION CALCULATORS!!

ELÉCTRICO UNIDAD DE CONVERSIÓN Ahora disponible en español también!

This site offers formulas for converting between electrical units. It is dedicated to sharing information, formulas and other documentation to aide in the conversion of given electrical, force or power values into other electrical, force or power values. The formulae below are commonly known and used universally. I use them here in examples to demonstrate the application of conversion formulae. I have done my best to be accurate but I cannot guarantee that all of the following information is correct or appropriate for your purposes.

I welcome any comments or corrections. Thanks to all who have notified me of inaccuracies. This type of participation makes this site more valuable. Please click here for a link to email your comment, correction, suggestion or question.

How to convert Watts to Amps

Basics

You cannot convert Watts to Amps, since Watts are power (ultimately horsepower) and Amps are current (or flow if you like) unless you have the added element of Voltage to complete the equation. You must have at least least two of the following three: Amps, Volts and Watts, to be able to calculate the missing one. Since Watts are Amps multiplied by Volts, there is a clear relationship between them.

Click here to see my Ohm's Law Pie Chart that shows the relationships between power (P), Voltage (E), current (I) and resistance (R) .

Choose Your Topic Below

Three Phase Power

Computing Watts
Computing Volt-Amps
Computing Kilovolt-Amps
Computing KiloWatts
Converting Between kW and kVA
Computing kBTUs

Short and sweet formulae:

Convert kVA to Amps
Convert Watts to Volts
Convert Watts to Amps
Convert Amps to Watts
Convert Horsepower to Amps

Convert kW to Amps
Convert kW-Hours to kVA

HOW TO FIND AMPS
HOW TO FIND WATTS
HOW TO FIND KILOWATTS
HOW TO FIND KILOVOLT-AMPS
HOW TO FIND HORSEPOWER
HOW TO FIND KILOWATT-HOUR

Go to the Shotgun Section and browse

Go to the Shotgun Table of Formulae

A tiny bit of Mechanical and Motors (See our NEW Mechanical and Motors page for more)

Basic Horsepower Calculations

Energy Measurement with Joules and Dynes

Introduction

You may need to convert Voltage, Amperage and electrical specifications from equipment into kW, kVA and BTU information that can be used to calculate overall power and HVAC requirements. The following section addresses the process of taking basic electrical values and converting them into other types of electrical values.

The specification nameplates on most pieces of computer, radio or network equipment usually list required electrical power values. These values are usually expressed in volts, amps, kilovolt-amps (kVA), Watts or some combination of all of the above.
If you are an architect or engineer using equipment nameplate information to compute power and cooling requirements, you will find that the total power and cooling values will exceed the actual run requirements of the equipment. Reason: the nameplate value is designed to ensure that the equipment will start and run safely. Manufacturers build in a "safety factor" (sometimes called an "engineering cushion") when developing nameplate specifications. Some nameplates specify power requirements that are higher than the equipment will ever need. The most common engineering solution is to utilize only 80% of available capacity and therefore your computed results will overstate the power and cooling equipment requirement by a factor close to 20%.

Develop the power and cooling budget using the nameplate specifications inserted into the formulae below and use the resultant documentation as your baseline. Document everything. There will come a day when you will need every amp of power you projected. Power budgets are notoriously consumed in a much shorter time than predicted. Don't forget to add a "future factor" to your power and cooling budget. Power supplies double in power draw and heat output every two to three years. If you don't include these factors in your budgets, you will consume a 10 year power and cooling budget in three years (this happened to me, I know this is true).

Three Phase Power

You will notice that all of the equations that refer to three phase power contain the value 1.73 in the formula somewhere. The value 1.73 is the square root of 3. Intuitively, you can see how this value is applied in the formulae. (3 phases therefore 1 phase = square root of 3)

Computing Watts When Volts and Amps are Known

POWER (WATTS) = Volts x Amps

For example, a small computer has a nameplate that shows 2.5 amps. Given a normal 120 Volt, 60 Hz power source and the ampere reading from equipment, make the following calculation:

POWER (WATTS) = 2.5Amps x 120Volts = 300 WATTS

Generally: P=IE

P= Power(WATTS)

I = Current(Amps)

E = Voltage(Volts)

So: I = P/E and E = P/I
Therefore: 1 Watt = 1 Ampere x 1 Volt

Click here to see my Ohm's Law Pie Chart for complete relationships between power, current and voltage.

Computing Volt-Amps (VA)

Same as above. Volt-Amps (VA) = Volts x Amps = 300 VA

Computing Kilovolt-Amps (kVA)

kVA stands for "Thousand Volt-Amps".

A 2-Pole Single Phase 208-240 power source requires 2 hot wires from 2 different circuits (referred to as poles) from a power distribution panel.

SINGLE PHASE

       KILOVOLT-Amps (kVA) = Volts x Amps / 1000

        Using the previous example: 120 x 2.5 = 300 VA       300 Va / 1000 = .3 kVA

208-240 SINGLE-PHASE (2-POLE SINGLE-PHASE)

Example: An enterprise computer bvserver with a 4.7 amp rating and requiring a 208-240 power source. Use 220 volts for our calculations.

        kilovolt-Amps (kVA) = Volts x Amps /1000

        220 x 4.7 = 1034          1034 / 1000 = 1.034 kVA

THREE-PHASE

Example: A large disk storage system loaded with disks. The equipment documentation shows a requirement for a 50-amp 208-240 VAC power source. Do not calculate any value for the plug or receptacle. Use 220 volts for the calculation.

kilovolt-Amps (kVA) = Volts x Amps x 1.73 / 1000

220 x 50 x 1.73 = 19,030 19,030 / 1000 = 19.030 kVA This would be rounded to 19

Computing KiloWatts

Finding KiloWatts requires using a power factor in the computation. The power factor is a number that adjusts the power calculation to reflect the efficiency of the use of the electricity supplied to the system. This factor can vary widely (usually from 60% to 95%) and is never published on the equipment nameplate and is not often supplied with product information. For purposes of these calculations, we use a power factor of .85. This random number places a slight inaccuracy into the numbers. Its OK and it gets us very close for the work we need to do. Most UPS equipment will claim a power factor of 1.00. It is common for the power factor to be considered 1.0 for devices less than 3 years old.

SINGLE PHASE

Example: We have a medium-sized Intel server that draws 6.0 amps and the power supply has a power factor of .85.

        kiloWatt (kW) = Volts x Amps x Power Factor / 1000

        120 x 6.0 = 720 VA       720 VA x .85 = 612      612 / 1000 = .612 kW

208-240 SINGLE-PHASE (2-POLE SINGLE-PHASE)

Example: An enterprise computer server has a 4.7 amp rating and requires a 208-240 power source. I'll use 220 volts and a power factor of .85 for our example calculations.

        kiloWatt (kW) = Volts x Amps x Power Factor x 2 / 1000

        220 x 4.7 x 2 = 2068          2068 x .85 = 1757.8      1757.8 / 1000 = 1.76 kW

THREE-PHASE

Example: A large storage system loaded with disks. The equipment documentation shows a requirement for a 50-amp 208 VAC Power source. Do not calculate any value for the plug or receptacle. Use 220 volts for the calculation.

kiloWatt (kW) = Volts x Amps x Power Factor x 1.73
1000

220 x 50 x .85 x 1.73 = 16,175.50 16,175.50/1000 = 16.175 kW

To Convert Between kW and kVA

The only difference between kW and kVA is the power factor. The power factor, unless taken from the manufacturer's specifications, is an approximation. For this example, we use a power factor of .95. The kVA value will always be larger than the value for kW.

kW to kVA kW / .95 = kVA
kVA TO kW kVA x .95 = kW

To Convert Between kW-Hours and kVA

There is NO conversion from kWH to kVA. These are two different measures. kWH is energy and kVA is power (not necessarily dissipated). If you look at kW (power) and kVA (power), then there is a relationship. That relationship is the power factor of the load.

Computing BTUs

Known Standard: 1 kW = 3413 BTUs (or 3.413 kBTUs)
If you divide the electrical nameplate BTU value by 3413 you may not get the published kW value. If the BTU information is provided by the manufacturer, use it, otherwise use the above formula.

Shotgun Section

Here are conversions, short and sweet:

To convert kVA to Amps:
Multiply kVA by 1000/voltage [ (kVA x 1000) / E ]
For 3 Phase power divide by 1.73 [ (kVA x 1000) / E x 1.73 ]
To convert Watts to Volts when amps are known:
Voltage = Watts / Amps
E = P / I
To convert Watts to Amps when volts are known:
Amps = Watts / Voltage
I = P / E
For 3 Phase power divide by 1.73
To convert Amps to Watts when volts are known:
Watts = Voltage x Amps
P = E x I
For 3 Phase power multiply by 1.73
To convert Horsepower to Amps:
Horsepower = (E x I x EFF) / 746
Efficiency = (746 x HP) / (V x A)

Multiply Horsepower by 746W (1 HP = 746 Watts)
Find Circuit Voltage and Phase

Example:
40 HP at 480 (3 Phase) 746 multiplied by 40 = 29,840
29,840 divided by 480 (3 Phase) = 62.2
62.2 divided by 1.73 = 35.95Amps
To convert kW to Amps:
Multiply kW by 1000/voltage and then by Power Factor [ (kW x 1000) / E x PF ]
for 3 Phase power divide by 1.73 [ ( kW x 1000) / E x PF x 1.73 ]

Shotgun Table of Formulae

HOW TO FIND Amps (I)
	Direct Current
	When HP, E and EFF are known:	HP x 746 / E x EFF

	When kW and E are known:	kW x 1000 / E

	SINGLE PHASE
	When P, E and PF are known:	P / E x PF

	When HP, E, EFF and PF are known:	HP x 746 / E x EFF x PF

	When kW, E and PF are known:	kW x 1000 / E x PF

	When kVA and E are known:	kVA x 1000 / E

	THREE PHASE
	When P, E and PF are known:	P / E x PF x 1.73

	When HP, E, EFF and PF are known:	HP x 746 / E x EFF x PF x 1.73

	When kW, E and PF are known:	kW x 1000 / E x PF x 1.73

	When kVA and E are known:	kVA x 1000 / E x 1.73
	(See abbreviations explained below)

HOW TO FIND WATTS (P)

	When E and I are known:	I x E

	When R and I are known:	R x I²

	When E and R are known:	E² / R
	(See abbreviations explained below)

HOW TO FIND KILOWATTS (kW)
	Direct Current
	E and I must be known:	E x I / 1000

	SINGLE PHASE
	E, I and PF must be known:	E x I x PF / 1000

	THREE PHASE
	E, I and PF must be known:	E x I x PF x 1.73 / 1000
	(See abbreviations explained below)

HOW TO FIND KILOVOLT-Amps (kVA)
	SINGLE PHASE
	E and I must be known:	E x I / 1000

	THREE PHASE
	E and I must be known:	E x I x 1.73 / 1000
	(See abbreviations explained below)

HOW TO FIND HORSEPOWER (HP)
	Direct Current
	E, I and EFF must be known:	E x I x EFF / 746

	SINGLE PHASE
	E, I, PF and EFF must be known:	E x I x PF x EFF / 746

	THREE PHASE
	E, I, PF and EFF must be known:	E x I x PF x EFF x 1.73 / 746
	(See abbreviations explained below)

HOW TO FIND KILOWATT-HOUR (KwH)
	BTU * (2.9307 * 10 ^-4)
	FtLb * (3.7661 * 10 ^-7)
	Joule * (2.7777 * 10 ^-7)

WHERE:

	E = VOLTS
	P = WATTS
	R = OHMS
	I = AMPS
	HP = HORSEPOWER
	PF = POWER FACTOR
	kW = KILOWATTS
	kVA = KILOVOLT-AMPS
	EFF = EFFICIENCY (decimal)

Basic Horsepower Calculations

Horsepower is work done per unit of time. One HP equals 33,000 ft-lb of work per minute. When work is done by a source of torque (T) to produce (M) rotations about an axis, the work done is:

radius x 2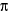 x rpm x lb. or 2 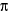TM

When rotation is at the rate N rpm, the HP delivered is:

HP = radius x 2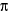 x rpm x lb. / 33,000 = TN / 5,250

For vertical or hoisting motion:

HP = W x S / 33,000 x E

Where:

W = total weight in lbs. to be raised by motor
S = hoisting speed in feet per minute
E = overall mechanical efficiency of hoist and gearing. For purposes of estimating
E = .65 for eff. of hoist and "connected gear."

Energy measurement with Joules and Dynes

Energy is measured in joules (Watt-seconds) or kiloWatt-hours. A power level of one Watt that continues for one second equals one joule. The integrated energy from a 100-Watt light that runs for 60 seconds equals 6000 joules.

4.18 joules equal 1 calorie, which is enough energy to raise the temperature of one gram of water by one degree Celsius (or Centigrade).

When it comes to energy density (Watts per liter or Watts per kilogram) it is difficult to beat gasoline. A lead-acid battery is good for about 125 thousand joules per kilogram. Lithium batteries can provide as much as 1.5 million joules per kilogram. Gasoline tends to run about 45 million joules per kilogram.

Joules:

1 joule is exactly 10⁷ ergs.

1 joule is approximately equal to:

6.2415 x 10¹⁸ eV (Electron Volts)
0.2390 cal (calorie) (small calories, lower case c)
2.3901 x 10⁻⁴ kilocalorie, Calories (food energy, upper case C)
9.4782 x 10⁻⁴ BTU (British thermal unit)
0.7376 ft-lb (foot-pound force)2.7778 x 10⁻⁷ kiloWatt hour
2.7778 x 10⁻⁴ Watt hour

Units defined in terms of the joule include:

1 thermo chemical calorie = 4.184 J
1 International Table calorie = 4.1868 J
1 Watt hour = 3600 J
1 kiloWatt hour = 3.6 x 10⁶ J (or 3.6 MJ)
1 ton TNT = 4.184 GJ

Useful to remember:

1 joule = 1 Newton meter = 1 Watt second

Dynes:

In physics, the dyne (symbol "dyn", from Greek δύναμις (dynamis) meaning power, force) is a unit of force specified in the centimeter-gram-second (CGS) system of units, a predecessor of the modern SI. One dyne is equal to exactly 10 micronewtons. Equivalently, the dyne is defined as "the force required to accelerate a mass of one gram at a rate of one centimeter per second squared":

1 dyn = 1 g x cm/s² = 10 - 5 kg x m/s² = 10 µN

The dyne per centimeter is the unit usually associated with measuring surface tension. For example, the surface tension of distilled water is 72 dyn/cm at 25°C (77°F).

**Units of force**
	newton (SI unit)	dyne	kilogram-force, kilopond	pound-force	poundal
1 N	= 1 kg x m/s²	= 10⁵ dyn	≈ 0.10197 kp	≈ 0.22481 lb_f	≈ 7.2330 pdl
1 dyn	= 10^-5 N	= 1 g x cm/s²	≈ 1.0197 x 10^-6 kp	≈ 2.2481 x 10^-6 lb_f	≈ 7.2330 x 10^-5 pdl
1 kp	= 9.80665 N	= 980665 dyn	= g_nx (1 kg)	≈ 2.2046 lb_f	≈ 70.932 pdl
1 lb_f	≈ 4.448222 N	≈ 444822 dyn	≈ 0.45359 kp	= g_n x (1 lb)	≈ 32.174 pdl
1 pdl	≈ 0.138255 N	≈ 13825 dyn	≈ 0.014098 kp	≈ 0.031081 lb_f	= 1 lb x ft/s²
The value of g_n as used in the official definition of the kilogram-force is used here for all gravitational units.

Mechanical

General Approximations - RULES OF THUMB

Use these in the field for fast approximations:

At 3600 rpm, a motor develops a 1.5 lb-ft of torque per HP at rated HP output
At 1800 rpm, a motor develops a 3 lb-ft of torque per HP at rated HP output
At 1200 rpm, a motor develops a 4.5 lb-ft of torque per HP at rated HP output
At 900 rpm, a motor develops a 6 lb-ft of torque per HP at rated HP output

At 575 volts, a 3-phase motor draws 1 AMP per HP at rated HP output
At 460 volts, a 3-phase motor draws 1.25 AMP per HP at rated HP output
At 230 volts a 3-phase motor draws 2.5 AMP per HP at rated HP output

At 230 volts, a single-phase motor draws 5 AMP per HP at rated HP output
At 115 volts, a single-phase motor draws 10 AMP per HP at rated HP output